剑指Offer 68-II 二叉树的最近公共祖先
1. 题目概览
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
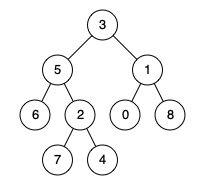
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉树中。
2. 解题思路
2.1 方法一:递归查找
在Offer-68-I中,我们分析过,对于二叉搜索树的中序遍历而言,祖先结点必然满足 $$ \min(p,q) \leq ancestor \leq max(p,q) $$
由于我们现在的树并没有搜索二叉树的性质,但我们仍然可以从中借鉴规律。若我们对树的中序遍历进行编号,令left为p、q中编号最小的,right为p、q中编号最大的,令祖先为mid,有: $$ left \leq mid \leq right $$
因此,公共祖先只有三种情况:
- $ mid == left $
此时,可以知道公共祖先的判断条件为:
(mid == left) && (mid.right 包含 right) - $ mid == right $
此时,可以知道公共祖先的判断条件为:
(mid == right) && (mid.left 包含 left) - $ left < mid < right $
此时,可以知道公共祖先的判断条件为:
(mid.left 包含 left) && (mid.right 包含 right)
因此,我们可以通过递归求解,由于递归是从叶子结点开始回溯,所以第一个符合条件的必然是公共祖先。
class Solution {
private TreeNode ans;
public Solution() {
this.ans = null;
}
private boolean dfs(TreeNode root, TreeNode p, TreeNode q) {
if (root == null) return false;
boolean lson = dfs(root.left, p, q);
boolean rson = dfs(root.right, p, q);
// 情况3 || 情况1、2
if ((lson && rson) || ((root.val == p.val || root.val == q.val) && (lson || rson))) {
ans = root;
}
return lson || rson || (root.val == p.val || root.val == q.val);
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
this.dfs(root, p, q);
return this.ans;
}
}
2.2 方法二:哈希法
先寻找p结点,记录他的所有父节点。然后寻找q结点, 返回时查找有没有该节点。
class Solution {
Map<Integer, TreeNode> parent = new HashMap<Integer, TreeNode>();
Set<Integer> visited = new HashSet<Integer>();
public void dfs(TreeNode root) {
if (root.left != null) {
parent.put(root.left.val, root);
dfs(root.left);
}
if (root.right != null) {
parent.put(root.right.val, root);
dfs(root.right);
}
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
dfs(root);
while (p != null) {
visited.add(p.val);
p = parent.get(p.val);
}
while (q != null) {
if (visited.contains(q.val)) {
return q;
}
q = parent.get(q.val);
}
return null;
}
}
2.3 方法三:转化成交叉链表
由于存在公共祖先,那么在前往p、q的路径上,必然会有相同的一段。如果我们只将达到p、q的路径画出来,就会发现这是一个类似交叉链表的结构。那么,我们要找的公共祖先,就是这个交叉链表的交叉点。所以对交叉链表的方法,对这个情况也适用。唯一的区别在于,我们的方向不同。
public class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//根节点到p节点的路径
List<TreeNode> path1 = new ArrayList<>();
//根节点到q节点的路径
List<TreeNode> path2 = new ArrayList<>();
getPath(root,p,path1);
getPath(root,q,path2);
TreeNode result=null;
int n = Math.min(path1.size(),path2.size());
//保留最后一个相等的节点即为公共节点
for(int i=0;i<n;i++){
if(path1.get(i)==path2.get(i)) {
result = path1.get(i);
break;
}
}
return result;
}
//前序遍历搜索节点p或q
void getPath(TreeNode root,TreeNode node,List<TreeNode> path){
if(root==null)
return ;
path.add(root);
if(root == node)
return ;
if(path.get(path.size()-1)!=node){
getPath(root.left,node,path);
}
if(path.get(path.size()-1)!=node){
getPath(root.right,node,path);
}
if(path.get(path.size()-1)!=node){
path.remove(path.size()-1);
}
}
}